2021-Hierarchical Core Maintenance on Large Dynamic Graphs
第一次组会讲的内容,论文的核心部分都放在下面的ppt中了,根据PPT做一些补充。
发表:VLDB2021
研究问题:动态图下的层次化核维护,即k-core的层次化结构树
*Page3:*
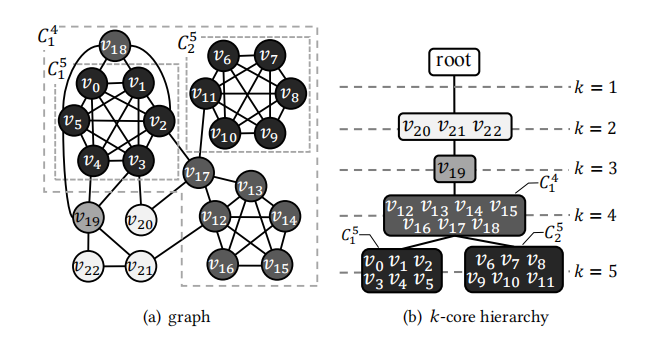
如下图所示,也如PPT中图3所示,每一棵Core Hierarchy Tree有三部分构成:
Node:$C_i^k$ 表示的对于每个k-core,其中间至少有一个顶点其core值为k的话,则这些$coreness=k$ 的顶点将会被命名为$n_1$ , 其代表的是一个顶点的集合,$n_1$也就是我们树上的节点
Edge: 树上的边表示为树上两个顶点$n_1$和$n_2$ ,其分别对应k1-core和k2-core,其二者在树中有边需要满足对应的三个条件
- $ k_1 < k_2 $
- $C_j^{k_2}$ 含于$ C_i^{k_1}$
- 不存在一个这样的$k_1<k’<k_2$ 使得$k’$ 可以成为$k_2$的父节点
Root: 最后则是root记录孤立顶点,并将其对应和最顶层节点建立边的关联
*Page4:*
这是一个例子,其中$v_20,v_21,v_22$的coreness都是2,所以去掉其以后原图成为一个连通的3-core,去掉v19则是一个连通的4-core,去掉右下方的$v_{12}-v_{17}$则不再连通,而是分别两个单独的5-core,其分别标记为$C_5^1,C_5^2$
*Page5:*
值得注意的是,这里删掉了$(v_2,v_{17})$这条边以后,原来的3-core结构则需要拆分成两个连通3-core,分别是$v_6-v_{17}$和$v_0-v_5,v_{18} v_{19}$,这里可以注意到$v_6-v_{11}$的父节点是$v_{17}$,而没有4-core这一层次上的节点
*Page6:*
首先是如何静态的构建一个k-core-hierarchy
输入是图,以及其degeneracy order的seq和顶点的coreness,输出则是对应的层次化树。
首先是声明一个空树,先为每个点在树中建立一个对应节点,对应权重为coreu。
*Page7:*
然后在seq中逆序遍历所有顶点,对每个顶点遍历其所有的邻居,若邻居之前没有在之前被访问,且其不属于同一个并查集。
则若其权重相同则将树中节点合并,否则指定小权重的为大权重的父亲,合并二者所在的并查集。
这个算法可以在O(m)的时间复杂度内生成一棵k-core-层次树
*Page8:*
这里引用了2017年的一篇论文,其在动态维护k-core上有一个很好的效果。
这篇论文大致是他给定每个点一个k-order,同一个$O_i$内的表示其core值均为i,但是其同一个$O_i$内的顺序是根据图k-core分解的动态算法得到的,也就是其在k-core分解中先被移除,其order就会更小。就像这个图分别维护了1-core,2-core,3-core.
然后如果要插入一条边,只需要在$O_k$中顺序的遍历,并根据他给的两个候选集条件来判断是否需要更新即可。然后同时需要维护这样的k-order序列。
*Page9:*
下面是算法部分,首先是处理插入的情况,单边插入下,当插入一条$(x_1, x_2)$的边时,我们取其中$x_1$和$x_2$更小的core值,设为K。
然后我们根据core值更新,可以总结出以下规律:
1)设定所有core值增加的顶点集为V, 则V中所有顶点的core值在更新前均为K,更新后均为K+1
2)无论插入两点的core值是否相等,可以得到V*的导出子图在G中一定连通。
这是因为我们知道插入一条边$(x_1, x_2)$时,只有与$x_1$连通且存在一条通路其上面的core值都为K时,这个顶点的core值才有可能会更新,而只有这条通路上的顶点均依次更新的时候,这个顶点的core值才一定会更新。因此这样就形成了一个连通图。
对x1=x2的core值时这个也是满足的。
*Page10:*
而对于k-core层次树来说,
1)对于core值大于K+1的,其在插入边后,每一个连通的k-core $C_i^k$其中的点都不会有core值的变化;同时也不会有新的点加入到这个集合中,因此其在k-core层次树上不会更新
2)对于k<= K 的 有两种情况 第一种是连通k-core $C_i^k$中包含了x1或x2中的一个,那么假设x1属于,$C_i^k$插入后会和x2所在的k-core连通
b) 或者若k=K ,则V*中的顶点的core值都会从K增加到K+1,这样的话,$C_i^k$中可能有部分顶点会更新到中$C_i^{k+1}$去
3) 第三种情况是,k=K+1,这样的话在V*中的顶点可能会将K+1层次内的k-core进行连接。
*Page11:*
首先$G_0[n_0]$表示的是在k-core层次树上,以$n_0$为根的子树的导出子图。
这个定理的意思是若$n_0$的子树导出子图与x1和x2所在的k-core没有交集,那么$n_0$所在的分支在k-core层次树上也不会有相应的更新。
证明是根据k-core分解的定义来的:让$k_0=core(n_0)$,由于更新k值更新的节点一定在$C(x_1) \cup C(x_2)$所在的导出子图中,而两者又没有交集,因此分解k0 的时候分解情况不变
这样的话,我们在更新k-core层次树的时候,只需要更新和x1,x2有关的子树部分即可。
*Page12:*
根据上述分析,首先我们先处理第二种情况,如何对k-core层次树中的祖先节点进行处理
我们设定$x_1$的core值更小,并设定为K。
第二行则是利用core值动态更新算法,更新所有受影响的节点的core值,并将这些节点放到V*中
$node(x_1, T_0)$表示在T0这棵树上,$x_1$所在的节点集合。我们对应初始化$x_1$和$x_2$在树上的节点集合。
之后采用了一种自底向上的合并过程,(4-13行)在T中递归合并$n_1$和$n_2$直到$n_1=n_2$
在每次迭代中,我们都记core值小的为$n_1$,否则交换$n_1$与$n_2$.
合并有两种情况,
1)若$n_1$,$n_2$的core值相等,因为其含有了$x_1$与$x_2$为连通图,则将其对应合并,将其父节点设定为$n_1$与n2的父节点中core值更大的呢一个,更新$n_1$,$n_2$为其父节点。
2) 若$n_1$的core值小于$n_2$,若$n_1$的core值小于$n_2$父节点的core值,则把$n_2$的父节点更新为$n_1$。最后更新$n_2$为其父节点
这个整体的过程很像LCA的操作。
*Page13:*
下面举一个例子,对于图a),其初始k-core层次树为$T_0$, 在插入了$(v_0, v_5)$这样一条边后,需要对应的更新,$n_1=v_5, n_2=v_0$
第一次迭代比较的是$node(v_5)和node(v_0)$ ,由于其core值不相等,且$v_0$的父节点core值更大,只将$node(v_0)$更新为$node(v_{15})$
第二次迭代比较的是$node(v_5)$和$node(v_{15})$ 由于core值不相等,但$v_5$core值大于$v_{15}$的父亲,因此将node($v_{15}$)的父亲更新为$node(v_5)$, $node(v_{15})$更新为$v_15$原来的父节点$node(v_{16})$
同上一次迭代的情况,这次是将$v_5$的父节点指向了$v_{16}$,然后$v_5$更新为root
最后一次$v_{16}$迭代为root,二者相等结束,更新后得层次树为$T_1$,这里只完成了对其父节点的更新,还没有对子节点进行操作。
*Page14:*
下面是如何调整子树部分,
首先做的是先证明所有core值被更新的点V*都在上一步的n1‘所在的子树中,且要调整的节点也都在这个子树中。也就是要证明定理2
首先对于第一个部分,也就是V*均在n1’的子树中:
若插入边$(x_1,x_2)$中 $core(x_1)<core(x_2)$ 那么$n_1’ = node(x_1,T_1)$ V*就包含在$node(x_1)$中
若$core(x_1,x_2) n_1’ =node(x_1) \cup node(x_2)$ ,V*在$V(n_1’)$中
第二部分,其仍然是依据了核分解的定义,若某节点所在子树的导出子图与$n_1’$所在的导出子图没有交集,则其在k-core层次树中保持不变。
*Page15:*
同时,我们可以证明V*必然被含在最终更新的k-core层次树中的一个节点内。
这是因为V*为连通图,且其中每一个顶点的core值均为K+1,
*Page16:*
下面是调整子树部分的代码,根据上述证明,我们知道了哪一部分的节点需要调整层数。
第14-17行为如何调整需要改变层数的节点。
$T_1=T$,也就是经过调整父节点后的树。首先是让n’ 即为含有$node(v^*)$在$T_1$中的节点。
之后是为每一个在T中为n’在第k+1层的子节点均创建一个新的节点n+,然后对所有的V*,都从n‘移动到N+中。
*Page17:*
首先我们定义cn,其表示的是以$n_0$为父节点的$nc$,且nc的子树中含有$v_0$这样的节点。
如右图所示$cn(n’,v_0) = node(v_{15})$
在此基础上,我们定义NC,其表明的是一个节点集合,其中每个节点都以$n_2’$为父节点,且其子树含有V*在原图的邻居中的一个节点。
如右图所示,$V*={v_5}$,其在原图的邻居为$(v_{11},v_6,v_0)$,则$NC(n2’,V*)={node(v_{11}), node(v_6),node(v_{15})}$
基于以上定义,我们证明定理4,也就是每一个NC中的节点,其所在的k-core层次树子树的导出子图都别涵盖在n*子树的导出子图中。
首先,根据NC的定义,因为n’的core值为K,而nc的父节点为n’,因此其core值均大于等于k+1.
其次,nc中存在一个顶点和n+中顶点相连,这是因为NC是通过V*中的邻居导出的,保证了其连通性。
这样的话,当nc的core值为k+1时,其应当与n+合并
或者其core值大于K+1时,n+就应当成为nc的一个祖先节点。因此证明了上述结论。
换句话说nc所在的节点应当在n*的子树中
*Page18:*
因此我们有这样的代码:
第17行先通过cn(n’,u)来提取所有的NC,然后对于NC中的每一个节点,
19-20行如果其为core值为k+1,那么将nc和n+合并
21-22行如果core值大于k+1,那么设置nc的父节点为n+
最后23-25行如果n‘中因为将所有的V*都移除变空了,那么对于n‘的所有子节点,都将其父节点置为n‘的父节点,删除n’即可。
*page19:*
前面的$cn(n_0,v_0)$的实现代码是这样的,给定$n_0,v_0$,我们将所有访问路径上的节点放到A中,然后设置$nc=n_1=node(v_0)$ nc为最终答案,在遍历中表示的是上一次的n1
当$n_1$不等于$n_0$时,就向上遍历即可,然后将访问过的节点放到A中,直到$n_1=n_0$,也就是nc的父节点为$n_0$
过程中用了一个Jump做记忆化,其表示的是若已经求过$cn(n_0,v_0)$则可以直接获得值
因此在求出nc后,需要将A中所有的节点,都设置其$cn(n_2,v_0)=nc$
****Page20:***下面举一个例子说明,前面我们插入$(v_0,v_5)$后得到了如$T_1$这样的一棵树,然后已知V={v5},那么我们建一个新的节点n+,并将n5,移入,同时我们根据NC的定义得到$NC={node(v_{11}),node(v_6),node(v_{15})}$
由于$node(v11),node(v_{15})和node(v_5)$ core值相等,因此合并
$node(v_6)和node(v_5)$core值不等,因此将$node(v_6)$的父节点指向$node(v_5)$
此时n’为空节点,对应将其子节点的指向更新即可。
****Page21:****这个是插入单边的完成更新算法,每一个部分前面讲过,主要思路就是先更新父节点,然后更新需要更改层级的节点,最后调整NC,也就是子节点。
****Page22:****复杂度分析
$O_k$表示core值为k的节点数, $k_max$为树的高度,第一部分复杂度为更新core值的复杂度,第二部分为merge最多的次数,也就是树的高度
*page23:*
后半部分的复杂度,一部分是将顶点从n+移动到n’
另一部分是遍历NC的复杂度,最多也就是node(x1)的子树+node(x2)的子树的大小
总时间复杂度为各部分加和
****page24:****多边插入
首先(2-3)行,是对每一条插入的边都做了一次core值更新
(4-6)行我们创建一个n*作为n‘的子节点,其中n’是至少含有一个V‘中顶点的节点
N表示为含有V‘中顶点的节点集合,其最后一定会被merge成一个节点。因此n‘可以设置成N中任意顶
之后我们需要枚举需要合并或更改指向的进入到候选集C中,第7行是将(n*,n0)更新到候选集中,这也就是需要子树调整的部分。
第八行则是对core值更新的节点都从n‘移动到了n+这样一个操作,这样所有需要调增层级的操作我们都做完了
对应我们将V*,G0更新
第11行则是因为插入一条边会导致部分节点的合并,放到候选集
13-15则是将所有的NC加入候选集
****page25:****例子,插入(v1,v14)没有节点更新
插入(v5,v16) V’={v16} ,因此为v16新创建一个节点,这个空集合为n’ ,n*=node(v16)
将(n’,n*) 加入候选集
根据算法我们需要将两条插入的边(node(v5),node(v16)), (node(v1),node(v14))加入候选集
最后则是v16的邻居(node(v5),node(v16))和(node(v16),node(v15))加入候选集
*Page26:*
下面我们对所有的候选集更新:
我们采取自底向上的方法,kmax代表core值最大的顶点
对core值为K的每次迭代,我们选取C中没有被访问过的顶点且core值为K的n0,
N1存储每个访问过的顶点,这些最终将被merge
N2存储有(n1,n2)属于C,且core(n2)<K,这些节点将成为n1的祖先。
然后遍历N1中没被访问过的节点n1,将P(n1)加入N2
若候选集中有和n1有关的(n1,n2)这样的pair
若core(n2)=K,那么n2加入n1;反之说明其为父子关系,加入N2
选取n’为N2中core值最大的节点,将所有的(n‘,n2)加入候选集之后处理
这一层就把所有的N1中合并成一个节点,并设置合并后的节点的父节点为n‘
*Page27:*
我们之前有三个个候选对
$( node(v_5),node(v_{16})) (node(v_{14}),node(v1)), (node(v_{16}) ,node(v_{15})$
这里前面的空集处理就是$v_{16}$直接指向root了
第一轮中
$N_1=node(v_1)$ 其父节点$node(v_{15})$加入$N_2$
$pair(node(v_1),node(v_{14}))$ 的core值不等,N2中加入$core(v_{14})$
这样的话就需要加入$pair(node(v_{15}),node(v_{14}))$
第二轮迭代 N1={node(v15),node(v14)} N2={node(v5),node(v16)
就会将node(v15)和node(v14)合并,
第三轮迭代就会合并对应的node(v5,v16)
*Page28:*
和插入类似,其首先分析了相关性质
对于core值仍然是,插入后会存在一个连通的V*其对应的core值从K变成K-1 其中K为插入边中core值小的那个顶点
*page29:*
其k-core层次树则是,core值大于K的无须更新
小于等于K的:
当core值小于K,可以保证其core值是不会改变的。但删除边可能导致V*中的顶点从K层移动到第K-1层
同时node(x1)和node(x2)可能失去连通性需要分裂。
****Page30:****与前面相反,删除时先维护的是子树部分
第二行代码首先还是计算更新的顶点V*
第三行则找到含有V的n‘ ,如果其父节点不是在K-1层,则创建一个n0在第K-1层,作为当前n‘的父节点,并将V移入;
若父节点在K-1层,直接将V*移入
移动完以后应当是原来含有V的node (n‘)其父节点为对应的n
*Page31:*
但这种移动可能会改变n’的连通性,因此我们需要做对应的分割。
split函数表明了如何分割一个nr的子树,
(2-4行)首先为每一个nr中的顶点都创建一个空节点将其移入,这样nr就成为了一个空节点。
为快速检测两个顶点是否在一个k-core中,使用cn(n0,v0),5-7行预先处理了nr子树的cn(nr,node(v0))
对于图中的每一条边(u,v)其中u属于分割前的nr中,若其core值相等,则可以合并;10-11行这样做的
12-16 若core(v)>core(u), 那么我们找到cn(nr,v)也就是nr子节点nc,且nc子树中含有v的这样节点。当P(nc)=nr的时候,我们设置P(nc)=node(u)因为这个时候nr为空了。
否则,我们将P(nc)与node(u)合并,因为P(nc)不等于nr说明前面已经更改过一次指向了,而P(nc)所指向的又能和node(u)连通,因次合并。
最后若仍然有指向nr的子节点,将其父节点改为nr的父节点,删除nr
*Page32:*
删除(v2.v17) 则对应的V*={v17} ,因此在对应的图a中,n’中的v17被移动到n*中去了。然后对应的n‘每个顶点都分成一个节点。
之后Vr中包含{v18,v12,v13,v14,v15,v16},遍历这些顶点,并对每个顶点遍历其的邻居节点
对v18来说,因为其和v0相连,node(v0)就指向了v17
v12,v13,v14,v15,v16因为彼此相连其被合并为了同一个顶点
最后node(v6)因为仍然指向n‘,则将其父节点改为node(v19) 删除n’
*page33:*
然后我们来看其父节点,从上个图可以看出,将v从n‘移动到n的行为不一定能保证n的连通,因此我们需要迭代的split n直到分割前后没有任何改变了
*Page34:*
这是他的总体代码,这题就是先调整V*,然后利用split不停往上调整即可。
*Page35:*
这是删除多条边的情况,他在这个地方的处理我觉得没什么大的改进。
第三行先是找到V,然后和前面一样,将每个V所在的node‘进行移动到上一层去
然后仍然是增加候选集{n’, n*}
根据core值从底向上的进行split操作,就完成了维护。
*Page36:*
选取了10个不同数据集,分别用加粗的字母来代替这个数据集,这里列举了其顶点,边数,平均度,最大core值和k-core层次树中节点个数
*page37:*
这个实验是第一列和第二列表示的是作者的算法在插入和删除的效率。
第四列LCPS是一个静态计算k-core层次化的算法。
LCPS+则是在LCPS利用动态维护k-core的算法合成的。
可以看出,在进行单边插入和删除的时候,明显作者提出的想过要好很多。
但是当有多边插入的时候,插入的效果依然很好,但是删除就不一定了
*Page38:*
这个表明了插入x条边的速率,这里插入确实比删除快很多,删除到2的6次方,已经要跑到1000s了,插入到1024条边也才不到10s
*Page39:*
最后想讲一下他的这个实验,他这个实验很好的表明了自己研究结果的作用。
他讲user engagement来在网络中量化,对DBLP数据集,每个作者被视为一个顶点,两个作者之间若为共同作者,则视为有边。
在几何中,顶点的交接指的是它们通过多边形或其他几何图形的边相互连接的方式。例如,如果两个顶点通过一条边相连,则称这两个顶点是“相接”的。通常情况下,顶点的交接是几何中的一个重要概念,因为它决定了几何图形的整体形状和结构。
树上节点的参与度是节点内部用户平均发表的论文数量。
作者认为k-core层次树不仅能提供k-core信息,其对应的位置也是很重要的。
作者会选取第K层子树最大的呢个节点,然后他比较比起parent的参与度更高的顶点数也就是T-edge
另一个是比较其和同一层中其他节点的参与度,同样接近百分之百,作者用这两个对比想表明,k-core层次树是有实际应用意义的。
*page40:*
最后总结,这篇论文研究的问题是维护动态图的k核层次树问题
作者提出了有效的局部更新策略,同时比现有方法更加有效;
且作者认为这种方法可能应用到其他分解,并为分布式的k-core层次维护提供可能。