2018-Cohesive Subgraph Computation over Large Sparse Graphs

本文是对该书的内容进行简单整理，全文过长，详细内容在PPT内，其中对各个章节的核心内容和算法将在下方进行简单说明分类。

第一章：

基础知识介绍：包括图的基本术语，相应数据集；以及相应的图算法的综述

第二章：

数据结构的介绍，皆为用来存储对应图结构的：

1. Linked List-Based Linear Heap

   

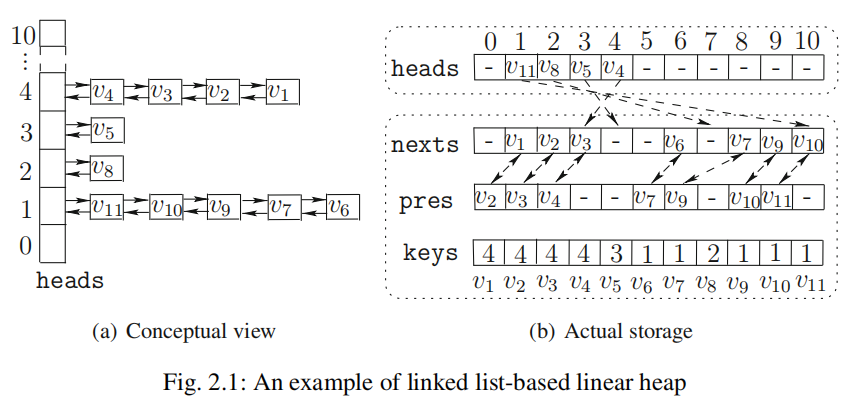
   其基本结构很简单，主要是用了双向链表的结构

   •heads：the heads of doubly linked lists

   •pres and nexts: the information of doubly linked lists

   •keys: the key values of all elements

​

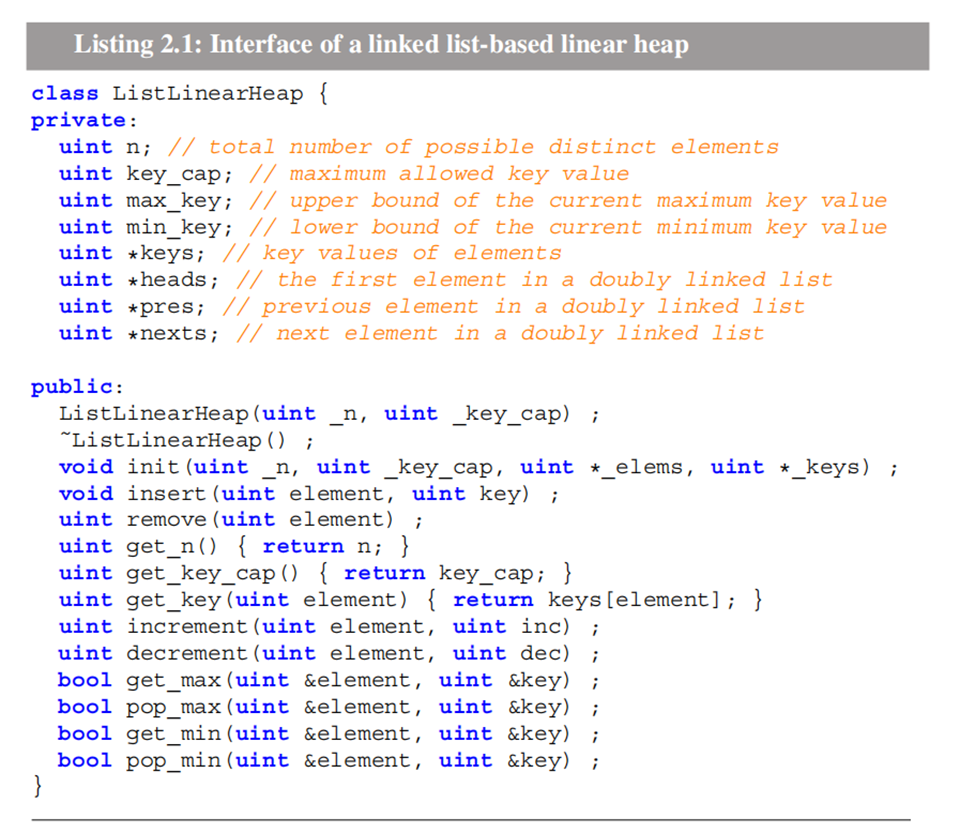
​ 对应支持的操作如上所示

2. Array-based Linear Heap

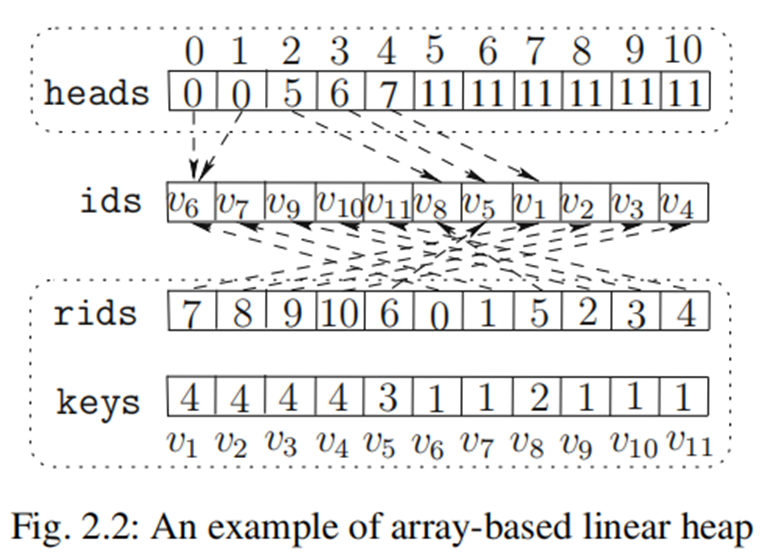
其转换成为数组的结构了，可以理解为按照key_value来排序的，有点像桶排序的感觉

•ids: all elements with the same key value are stored consecutively in an array ids

•heads: the start position of the elements for each distinct key value is stored in heads

•keys: the key values of all elements

•rids: the position of elements in ids are stored in an array rids (i.e., rids[ids[i]]=i).

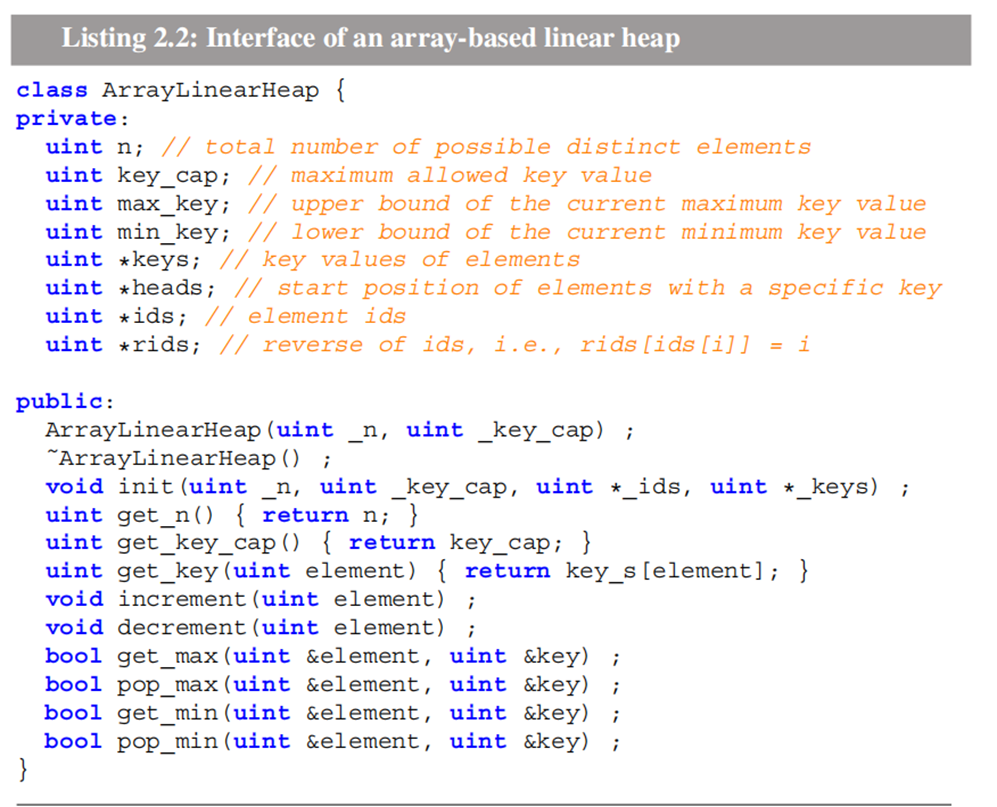
对应支持的操作如上

3. LazyLinearHeap

相比较前面的链表结构，其主要是改成了单向的链表，且在维护元素更改时，会用懒标记

​

第三章

主要是围绕着k-core的相关内容

1. 首先是k-core的定义部分：

   定义部分包括：

   1） k-core，如下图

   

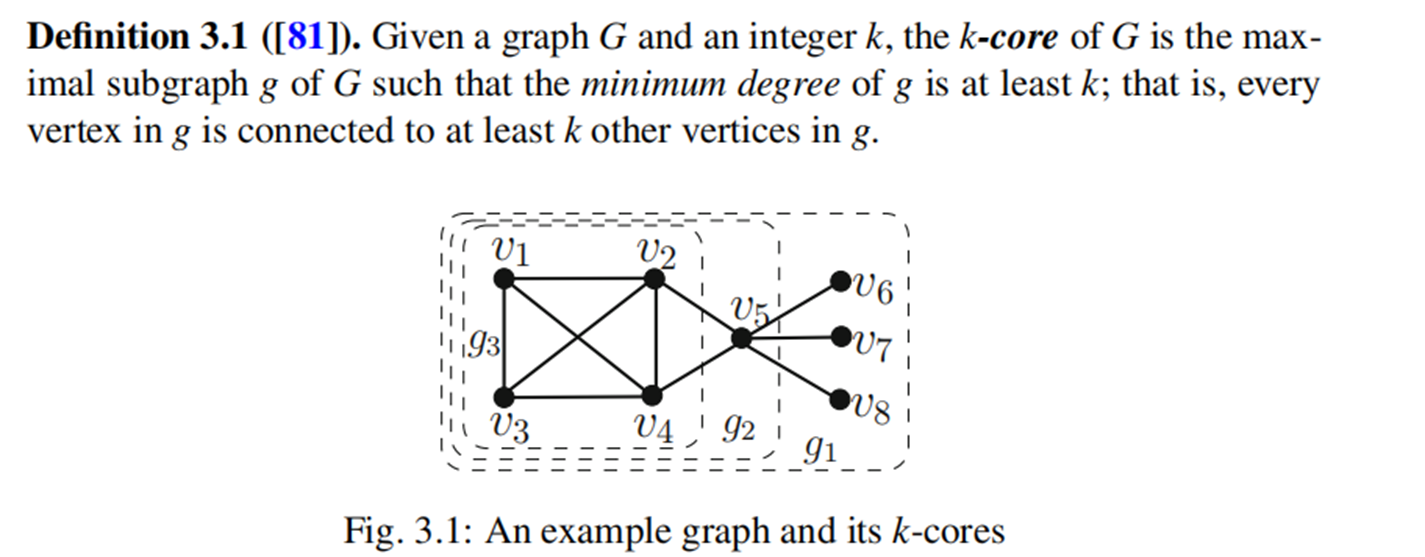
   2）顶点的core number，这也是通常k-core维护中维护的内容

   3）degenerarcy $\delta(G)$：表示的是G中每个子图每个顶点的度最多为k

   4） arboricity $\alpha(G)$: 表示的是G被分为最少的边不交的生成树的个数

2. k-core计算：

   1）Peel 算法：本质是逐步剥离当前core值最小的顶点，对应会根据剥离顺序得到 degeneracy ordering

   2）k-core计算：找到对应的子图

   和peel算法类似，无非是将对应的子图进行了存储

   3）Core Hierarchy Tree：

   定义时，增加了连通k-core的定义，这样使得层次树中含有连通性信息，建立时需要用到并查集的结构

   

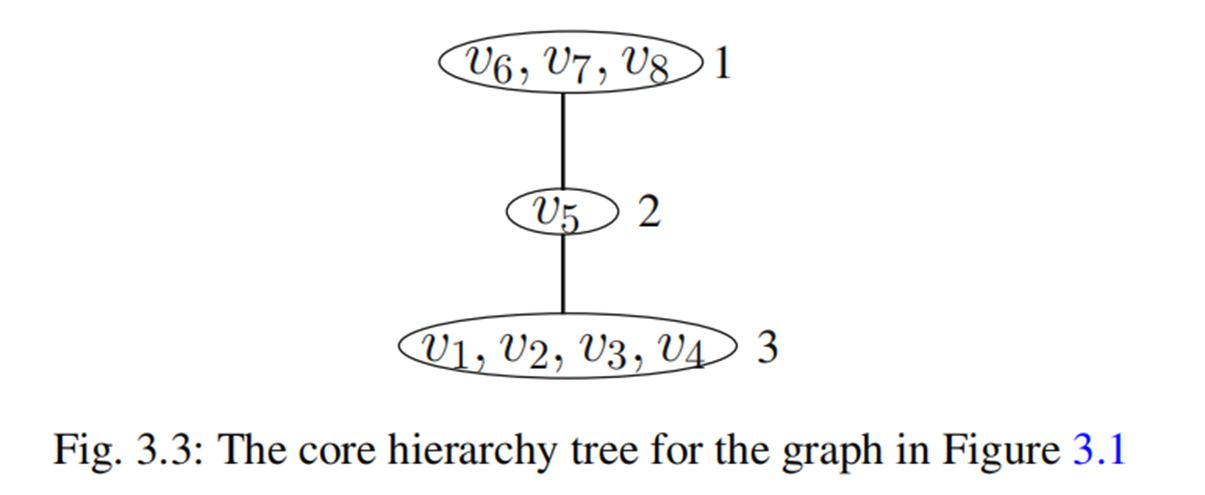
   当前针对于这个问题，已经存在了动态的维护方法，对应的分布式算法也有提出。

   4）Core Spanning Tree:

   

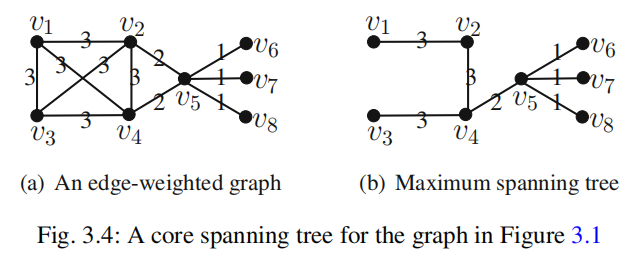
   $G_w$生成方式是参考最大生成树来的，其中每一条连通边的权值$w(u,v)$被定义为 $min{core(u),core(v)}$

   该问题意义：

   ①同时保留了k-core信息和对应的连通性信息，我们想提取最大的连通k-core时，只要保留最大的core值相连的边即可

   ②其可以用来做密度的近似，同样是用上面的办法，只保留最大的core，但是其中最后一个顶点需要重复加一遍前面的core值，然后最后将累计的权值除二再除以顶点数

   

3. 其他情况下的k-core分解

   1） An h-index-based Local Algorithm

   定义了一个h-index ，然后基于这个定义来分解k-core

   2）I/O- Efficient Core Decomposition

   基于IO加速的分解，其实就是一边读写一边做操作，少了一些邻居信息

第四章 最密子图计算

1. 定义部分：

   $\rho(g)= \frac{|E(g)|}{|V(g)|}= \frac{d_{avg}(g)}{2}$

   问题通常分为近似问题和精确问题

2. 近似问题：

   1）2-Approximation 算法

   直接按照degenerarcy ordering 剥离即可

   2） A straming $2(1+\epsilon)$- Approxiamtion 算法

   利用当前度来计算，每次剥离 $d(v)<= 2*(1+\epsilon) * \rho(S)$ 的顶点

   3） 精确算法：

   密度测试——利用网络流+二分的算法，合理建图来判断密度区间

第五章 高层结构的核分解

1. 3-clique(三角形分解)：

   

   本质很像暴力枚举，就是枚举顶点v，然后枚举v的邻居w，再枚举w的邻居u来判断是否和v相连

   TriE Algorithm：

   和上面算法很像，区别就是换了枚举v的次序，并且将原图变成了有向图

2. k-clique 枚举算法：

   本质和前面一样啊，就是dfs多了几轮

   

   k-clique-oriented: 则是基于了TriE的一个改进

3. k-truss：

   k-truss是基于边来定义的，其定义了每条边的supp支持度，也就是其参与构成三角形的个数

   然后k-truss则是一个子图中每条边都能参与构成至少k-2个三角形

   性质：

   1）每个k-truss都是（k-1）truss的子图

   2） 每个k-truss都是（k+1) core 的子图

   对应有每个边的truss number 的定义：表明的是含有该边的最大的k-truss

   计算方式：

   PeelTruss：

   

   剥离过程中涉及到三角形的计算，肯定复杂度要大于peelcore

4. s-clique support: r-clique中含有s-clique的数量

   对应的s-clique connected ： 两个r-clique都被含在s-clique中包含对应的clique

   k-（r,s)-nucleaus 的定义：

   1） 任意r-clique 其s-clique的support 一定大于等于k

   2） 任意的两个r-clique在s-clique中一定是连通的

   

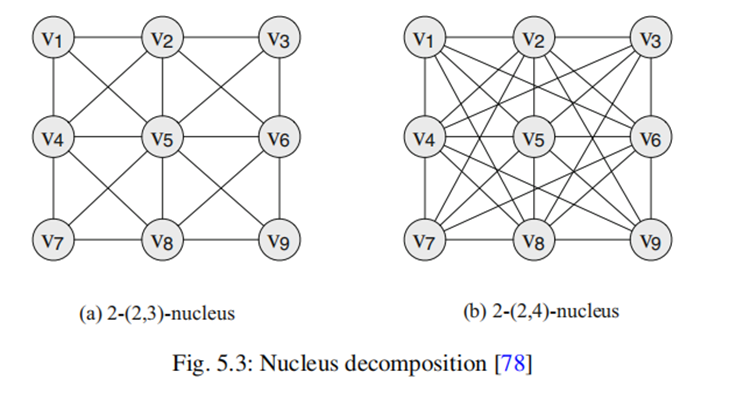
​ 计算：也是用的peelNucleus

​

5. k-clique density

   $\rho_k(g) = \frac{c_k(g)}{|V(g)|}, c_k(g)是g中k-cliques的数量$

   其计算密度对应也是近似算法和精确算法

第六章 边连通性分解

1. K-ECC 删除任意k-1条边以后仍然连通

   

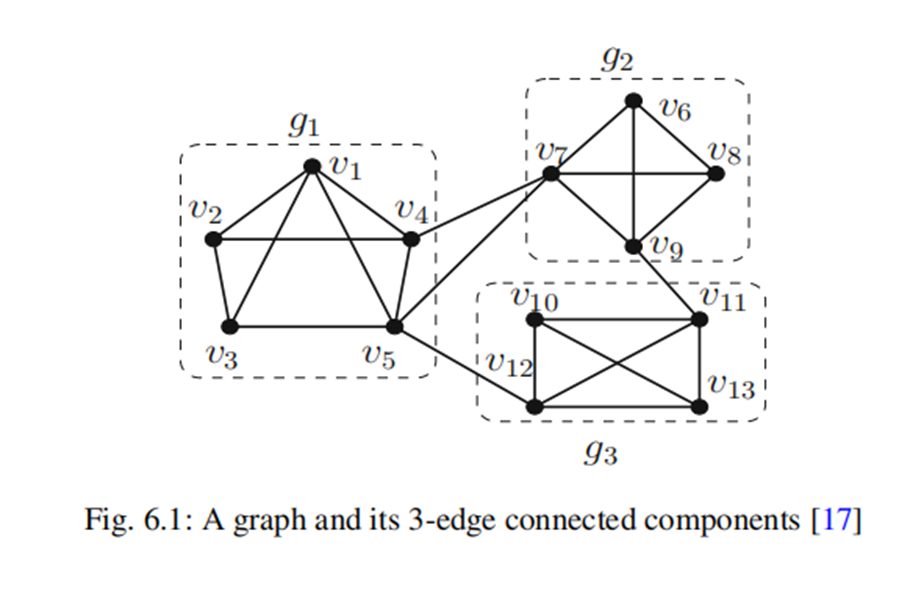
   计算方式KECC：

   

   这里面重点为如何分割

   1） 两路分割：

   

   其中计算最小割是通过下面的构造

   

   

   2） 多路分割