2019-Enumerating k-Vertex Connected Components in Large Graphs
这篇论文是围绕k-VCC的求解
一、Abstract部分:
1)研究问题:给定k,求出图中的所有K-VCC
2)k-VCC特性:高耦合、高鲁棒性、子图重叠性
3) 方法:
① 证明了分割问题的上界——可以用多项式时间来进行解决问题
② 提出了两个优化策略:neighbor sweep 和 group sweep
4)结果:
在大型数据集上证明了方法的高效性
有数量级的提升
二、Introduction部分:
k-VCC特性:
1) G的顶点连通性不大于边连通性和最小度
2) 直径较小
3) 子图的重叠性不超过n/2,其中n为顶点数
问题和现有方法:
1) 给定G和指定的k,求出所有的k-VCC
2) 现有方法:
递归的找到一个顶点小于k的顶点切割,并对图进行分区
一个顶点对的最小割是他们之间顶点独立路径的数量
本文方法:
1) 证明了k-VCC的数量不超过n/2 —— 因此可以用多项式时间来完成算法
2) Neighbor Sweep: 对一些顶点进行属性划分;一旦其被测试或swept,则对其所有邻居sweep;为顶点存一个值,结束测试为其周围邻居增加值,超过阈值则sweep掉
3) Group Sweep:将顶点划分为不相交的组,以组为单位进行上面的测试
贡献:
(1)一个多项式时间的算法
(2)两个有效的剪枝策略
(3)在实际问题的有效性
三、前置知识
定义1 : 顶点连通性k(G): 为移除最小数量的顶点导致原图不相连或成为平凡图
定义2: k-vertex-connected: (1) |V(G)|>k (2) 删除任意k-1个顶点后原图仍连通
定义3: k-vertex-connected-component
(1) g是k-vertex-connected (2) g is maximal
四、分割的基础框架
将原图分为t个连通块
对每个连通块都用GLOBAL-CUT来找点割集:
1)若点割集为空,则连通块本身就是一个VCC
2) 否则的话,kVCC将原图根据点割集分开,并将每一个分割后的子连通块再次递归调用KVCC-ENUM

五、Basic Solution
顶点割集计算:
Globla-cut的目的是计算出一个少于k个顶点的点割集
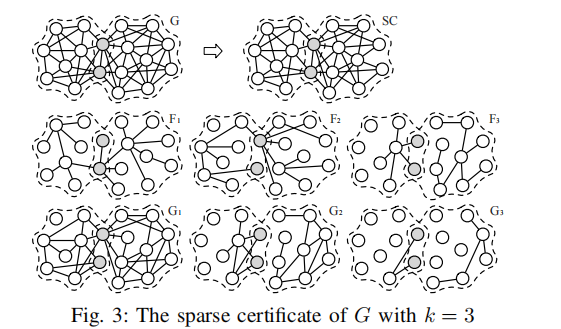
1) 先做一个sparse certification 的优化:将G提取其只有O(k.n)条边的k-vertex-connected连通的子图
2) 下面则分割根据u是否属于S(割集)进行分类讨论:
4-6行为不属于的情况,7-10 为属于的情况


具体需要结合上面的两个引理来进行理解,而LOC-Cut将原有的点拆点成为n+2m条边,2n个点的图,然后求u到v的最大流,即为其local connectivity

3) 整体时间度分析比较复杂: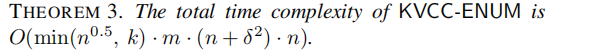
六、搜索剪枝
A. neighbor Sweep
- side-vertex: u不属于一个所含顶点小于k的割集S
- side-vertex u是可以传导k-vetex连通性的,进而减少了局部测试
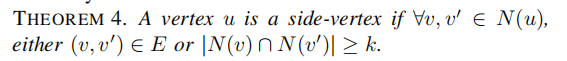
而其具体的求法则根据上面的定理得到
因为满足上面条件的为 strong-side-vertex,而这些点是可以传递k-vertex-connectivity,因此可以进行剪枝
其还可以利用Vertex Deposit进行维护
1) 若v可以和u的k个邻居都有k-vertex-connected,u和v也是k-vertex-connected的
2) 因此为每个顶点存一个deposit(v),表示其邻居节点中满足1)的条件个数的点
B. Group Sweep
首先是如何构造一个side-group
side-group定义如下:
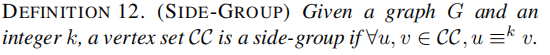
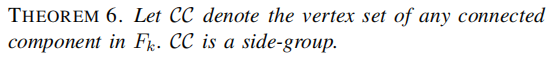
group sweep rule:
side-group 可以有以下的作用:
换句话就是group内一个side-vertex完成了测试,整个gorup的k-vertex-connected 性质就相同了

更一般的方法是,测试group里面是否有k个点均符合条件,并用deposit记录:
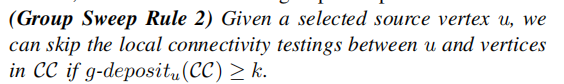
整体算法:

