研究问题：动态超图的超核维护

定义部分：

1）超图：一条边可以连接多个顶点

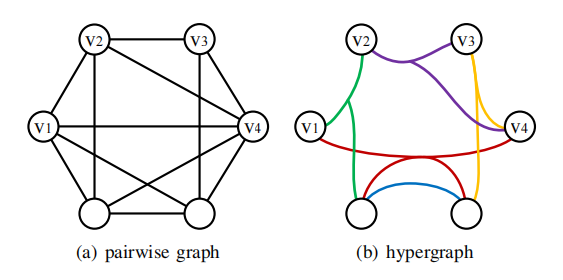
2）超核：和k-core的定义是一样的，只不过引入到了超图汇总

研究思路：

1）证明了单边插入和删除只会使得超核数量增加1或减少1

2）为超边提出了核的定义，同时提出了precore的定义，但两者都是为了实际问题服务

3）提出了支持度的定义
定义部分:

1）顶点和边的超核数定义：

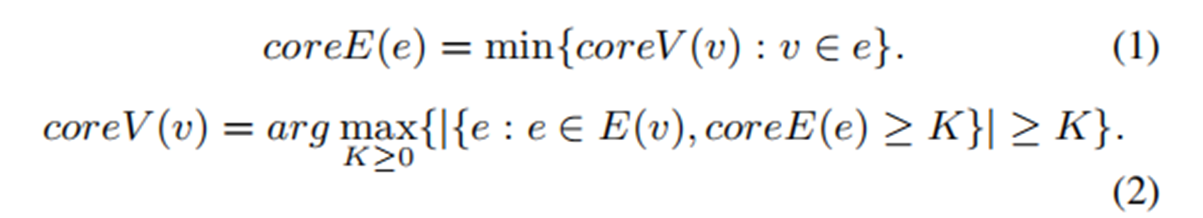
2） pre-core定义：新插入超边的最初超核数
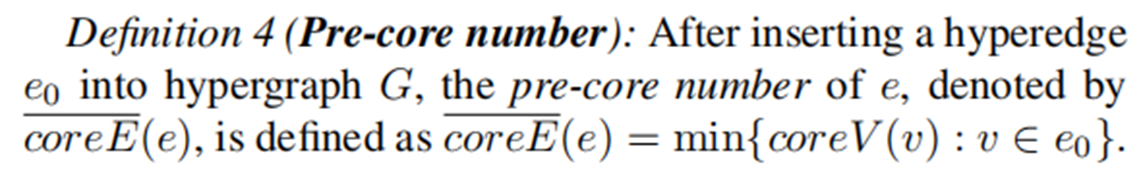
证明部分：

1）证明了插入超边和删除超边，只会对应使得顶点和边的超核数最多变化1

2）证明什么情况下，顶点和边的超核数会变化

插入时，只有$coreV(v)=\overline{coreE}(e_0)$ 时，顶点才可能增加超核数

只有$coreE(e)=\overline{coreE}(e_0)$时，边才可能增加超核数

同时，上面的顶点和超边必须在一条通路，且这个通路的顶点和边都是超核数满足上述要求，且起点为插入边$e_0$

删除时，只有$coreV(v)={coreE}(e_0)$时，顶点才可能减少超核数

只有$coreE(e)={coreE}(e_0)$时，边才可能减少超核数

同时，上面的顶点和超边必须在一条通路，且这个通路的顶点和边都是超核数满足上述要求，且起点为删除的边$e_0$
引入支持度的定义：

1）其定义如下：

本质是计算顶点中有多少条边能满足其更改core值

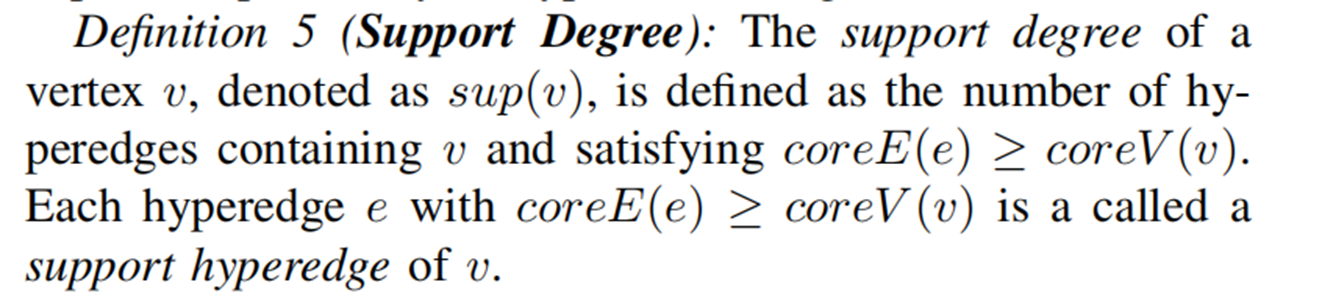
2）根据sup的定义来剪枝

只有满足下面条件的顶点才能有core值的变化
整体算法：

由于在超核维护前应该还有一个静态算法，来在O(m)的时间复杂度内计算出原始图的超核数量：

本质是peel算法，但是多了一个超边的超核数

时间复杂度：
实验部分：

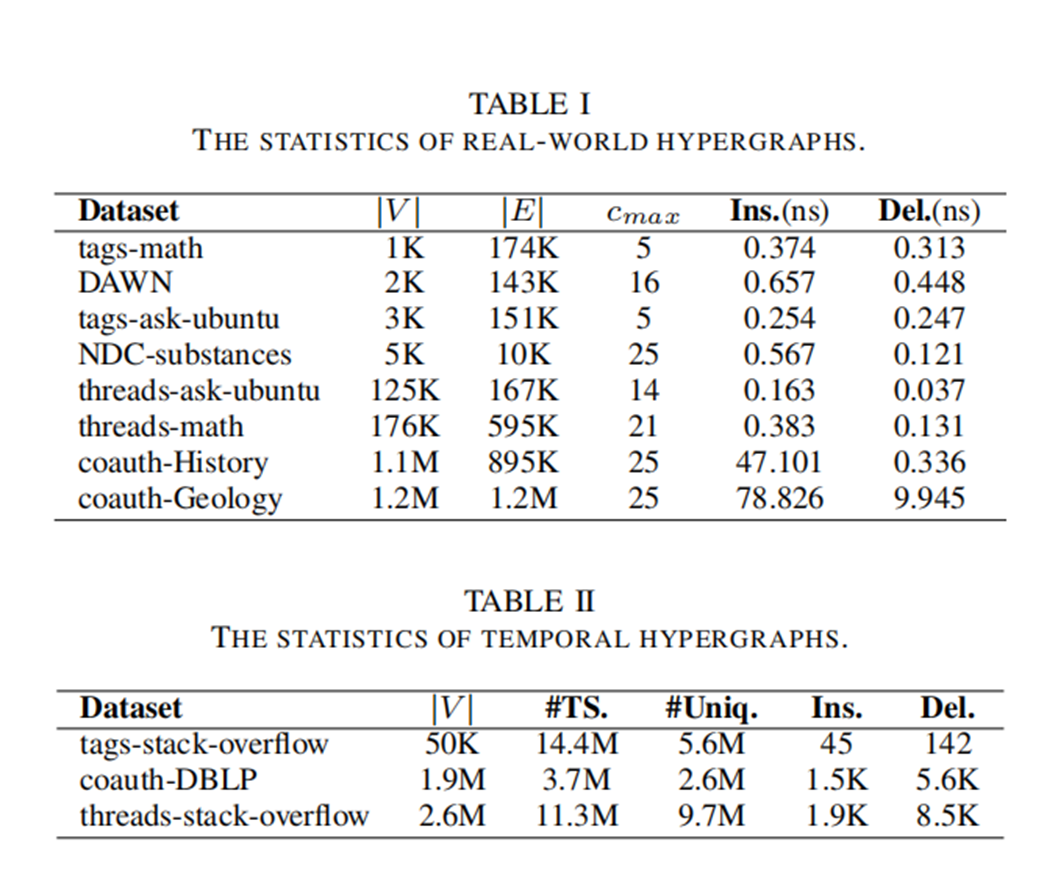
1）数据集和表现：

分为正常数据集和时序数据集

超图的构造和常规图是不同的，因为其超边需要连接多个顶点